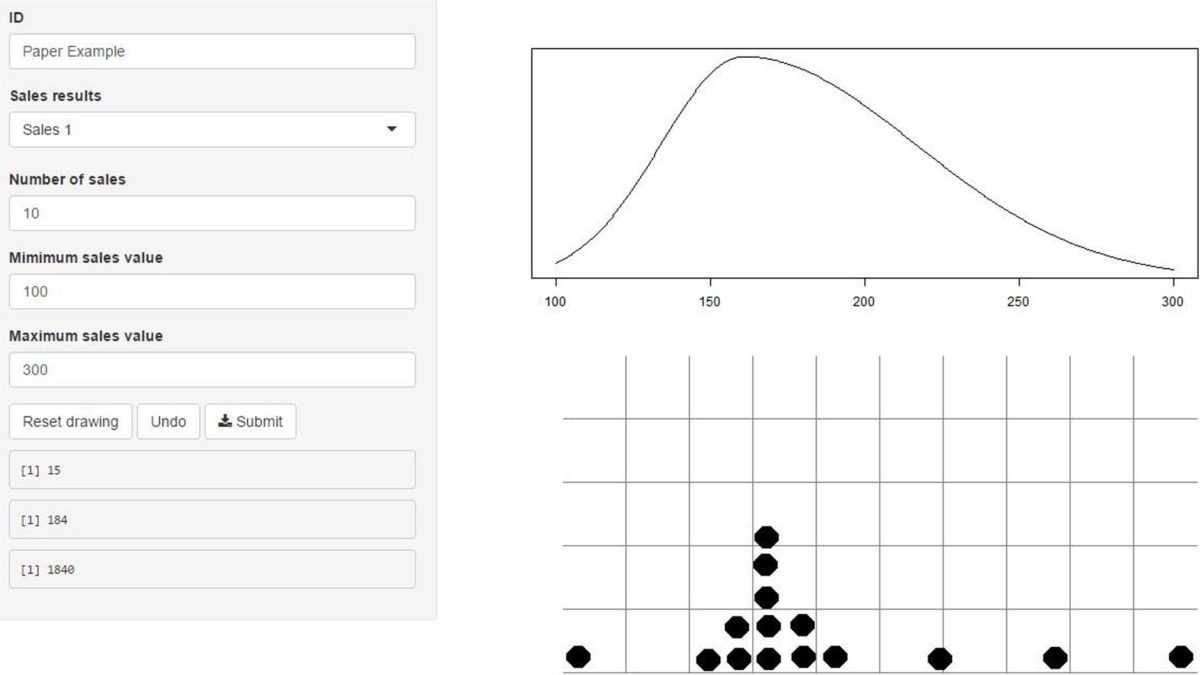
Elicitation is a commonly used tool to extract viable information from experts. The information that is held by the expert is extracted and a probabilistic representation of this knowledge is constructed. A promising avenue in psychological research is to incorporated experts’ prior knowledge in the statistical analysis. Systematic reviews on elicitation literature however suggest that it might be inappropriate to directly obtain distributional representations from experts. The literature qualifies experts’ performance on estimating elements of a distribution as unsatisfactory, thus reliably specifying the essential elements of the parameters of interest in one elicitation step seems implausible. Providing feedback within the elicitation process can enhance the quality of the elicitation and interactive software can be used to facilitate the feedback. Therefore, we propose to decompose the elicitation procedure into smaller steps with adjustable outcomes. We represent the tacit knowledge of experts as a location parameter and their uncertainty concerning this knowledge by a scale and shape parameter. Using a feedback procedure, experts can accept the representation of their beliefs or adjust their input. We propose a Five-Step Method which consists of (1) Eliciting the location parameter using the trial roulette method. (2) Provide feedback on the location parameter and ask for confirmation or adjustment. (3) Elicit the scale and shape parameter. (4) Provide feedback on the scale and shape parameter and ask for confirmation or adjustment. (5) Use the elicited and calibrated probability distribution in a statistical analysis and update it with data or to compute a prior-data conflict within a Bayesian framework. User feasibility and internal validity for the Five-Step Method are investigated using three elicitation studies.